シンプソンの多様度指数について

シンプソンの多様度指数（D)は、以下の式で求められます。

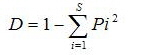
S=種数

Pi=相対優占度

相対優占度とは、それぞれの種が群集の中で、どれだけの割合を占めているか？ということを表したものです。

前ページの群集Aを例として考えてみます。

【群集Aの場合】

生物1：20個体

生物2：20個体

生物3：20個体

生物4：20個体

生物5：20個体

この時、生物1の個体数が全体の中で占める割合は

と求められ、生物1の相対優占度は0.2となります。

多様度指数の計算では、種iの相対優占度をPiと表して用います。

種iというのは、その調査で出現したそれぞれの種のことです。

シンプソンの多様度指数の示すところは、“調査で得られた個体すべての中から、ランダムに選んだ２つの個体が違う種である確率”です。

Σの右側はPiの２乗となっています。これは、相対優占度Piは全体の中で種iが占める割合なので、「調査で得られたすべての個体の中から、ランダムに一つの個体を選んだときに、種iを選ぶ確率」と言い換えられます。

これを２回試行して、どちらも同じ種になる確率は、Piの２乗をすべての種で計算し、それらを足した値になります。ただし、これは２回目を試行する前に、選んだ個体を元に戻して行っている場合の確率です。

この「２回試行して同じ種になる確率」は、種の多様性が上がれば上がるほど低い値を示します。分かりやすいように、これを1から引いて、「ランダムに選んだ２つの個体が違う種である確率」としています。

実際に計算してみましょう。

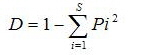
生物1～5の相対優占度は0.1であるため、

群集Aの多様度指数は0.8と非常に高い値となります。

【群集Bの場合】

生物1：1個体

生物2：1個体

生物3：1個体

生物4：1個体

生物5：96個体

この時、生物1の個体数が全体の中で占める割合は

と求められ、生物1の相対優占度は0.01となります。

さらに、生物5の個体数が全体の中で占める割合は

と求められ、生物5の相対優占度は0.96となります。

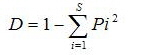
生物1～4の相対優占度は0.01、生物5の相対優占度は0.96であるため、

群集Bの多様度指数は0.078と非常に低い値となります。